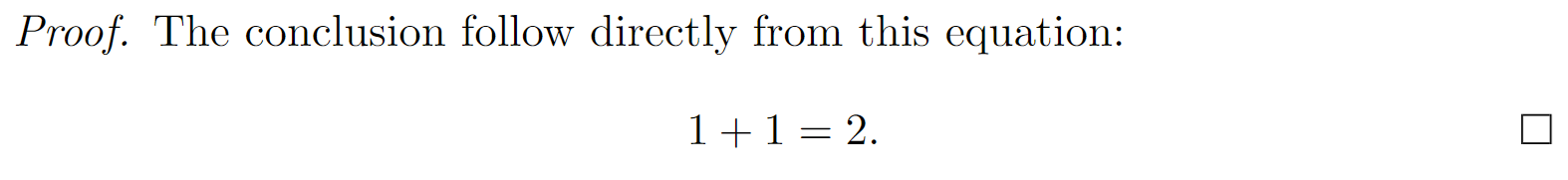Packages
To set up theorem-like environments, we load several packages in the preamble of the document.
amsthm Package
The amsthm package defines macros and environments for creating theorem-like environments.
\usepackage{amsthm}
hyperref Package
The hyperref package provides hyperlinking.
When hyperref is loaded, all references to theorem-like environments (inserted using \ref or \cref) automatically include links to the location where the environment is displayed.
You will likely want to modify some of the hyperref options.
% Enable hyperlinks
\usepackage{hyperref}
\hypersetup{
final, % Include links even if document is in 'draft' mode.
hidelinks, % Prevent boxes from being drawn around links in some viewers.
breaklinks=true, % Allow line breaks in the middle of links
colorlinks=true,
linkcolor=black, % TOC, links to labeled equations and environments
urlcolor=black!30!blue, % URLS including links in references
anchorcolor=blue, % I'm not sure what this does.
citecolor=black!30!blue, % In-line citations
}
cleveref Package
The cleveref package defines the \cref macro for inserting internal references to labeled object.
In contrast to \ref, \cref inserts the type of environment referenced, so a reference \cref{my first theorem} will appears as “Theorem 1”, whereas \ref{my first theorem} only appears as “1”.
% Display "Theorem 1", "Lemma 2", etc. in cross references.
% It's important to load this last after all the other packages!
\usepackage[
noabbrev, % E.g., "Figure" instead of "Fig."
capitalise, % E.g., "Figure" instead of "figure"
nameinlink % Make "Figure 1" linked instead of just "1".
]{cleveref}
Changing Theorem Body Text From Italic To Slanted
By default, the body amsthm theorem environments are italicized.
I find large chunks of italic text hard to read, so I create and use a different theorem style that uses slanted text instead.
This way, theorems are differentiated from surrounding text without compromising readability.
% Create a new amsthm theorem style that uses slanted text
% instead of italics. I find this makes the text easier to read.
% See https://tex.stackexchange.com/a/417959/153678.
\usepackage{amssymb} % Provides \slshape
\newtheoremstyle{sltheorem}
{} % Space above
{} % Space below
{\slshape} % Body font
{} % Indent amount
{\bfseries} % Head font
{.} % Punctuation after head
{ } % Space after theorem head
{} % Theorem head spec
% Enable the new "sltheorem" theorem style.
\theoremstyle{sltheorem}
Custom QED Marks at End of Environments
For long environments that are in upright font, I prefer to include a mark at the end of the environment to notify readers where the section ends.
The following command, \setEnvironmentQed allows for defining the QED-like symbol to automatically insert at the end of all environments of a given type.
For example, \setEnvironmentQed{definition}{\ensuremath{\blacksquare}} causes a black square to be inserted at the end of every definition environment.
% Define a macro for changing the QED symbol at the
% end of environments. This command allows for the
% use of \qedhere to insert the QED into, e.g.,
% equations or lists.
\newcommand{\setEnvironmentQed}[2]{
% #1: Environment name
% #2: QED Symbol. Must be OK in text or math mode.
% Use \ensuremath, if math is desired.
\AtBeginEnvironment{#1}{%
\pushQED{\qed}\renewcommand{\qedsymbol}{#2}%
}
\AtEndEnvironment{#1}{\popQED}
}
Here are several options for symbols that can be used to end environments:
| Symbol | LaTeX Code | Notes |
|---|---|---|
| \(\square\) | \square |
Traditionally used for the end of proofs |
| \(\blacksquare\) | \blacksquare |
|
| \(\triangle\) | \triangle |
|
| \(\blacktriangle\) | \blacktriangle |
|
| \(\triangledown\) | \triangledown |
|
| \(\blacktriangledown\) | \blacktriangledown |
|
| \(\circ\) | \circ |
|
| \(\bullet\) | \bullet |
|
| \(\diamond\) | \diamond |
\blackdiamond is not a built-in macro, nor provided by the amssym package. |
| \(\lozenge\) | \lozenge |
|
| \(\blacklozenge\) | \blacklozenge |
Environment Definitions
\providetheorem definition
In my LaTeX setup, I prefer to use the same preamble file for all of my documents, but I’ve found that some document classes or packages define theorem or other related environments.
To avoid errors when trying to define to new theorem-like environments, \providetheorem first checks whether the environment is defined.
% Create a new macro analogous to "\providecommand", which
% defines the given amsthm theorem-like environment only if
% it does not already exist.
\newcommand{\providetheorem}[2]{
% #1: Environment name.
% #2: Display name
\ifcsdef{#1}{
% The #1 environment is already defined.
\ifcsdef{end#1}{}{
\PackageError{providetheorem}{%
% Error message:
The command "#1" was already defined, but "#1end" was
undefined, indicating that "#1" is not an environment.
}{}
}
}{
% The #1 environment is not defined, yet, so we define it.
\newtheorem{#1}{#2}
}
}
Theorem Style
There are three default theorem styles: plain, definition, and remark, but I have replaced the plain style with sltheorem to use slanted text instead of italics.
The sltheorem (or plain) style displays a boldface label and slanted (or italic) body text.
\begin{theorem}[Pythagorean Theorem]
\label{result:pythagorean}
The sum of the squares of the legs of a right
triangle equals the square of the hypotenuse.
\end{theorem}

I use the theorem style for any environments that make truth claims, namely theorem, proposition, lemma, corollary, and conjecture.
%%--------------------------------------------------%%
%| Define environments that use the sltheorem style |%
%%--------------------------------------------------%%
\theoremstyle{sltheorem}%
%%% Define theorem environment %%%
\providetheorem{theorem}{Theorem}
\crefname{theorem}{Theorem}{Theorems}%
%%% Define proposition environment %%%
\providetheorem{proposition}{Proposition}
\crefname{proposition}{Proposition}{Propositions}%
%%% Define lemma environment %%%
\providetheorem{lemma}{Lemma}
\crefname{lemma}{Lemma}{Lemmas}%
%%% Define corollary environment %%%
\providetheorem{corollary}{Corollary}
\crefname{corollary}{Corollary}{Corollaries}%
%%% Define conjecture environment %%%
\providetheorem{conjecture}{Conjecture}
\crefname{conjecture}{Conjecture}{Conjectures}%
Definition Style
The definition style displays a boldface label and upright body text.
\begin{definition}
\label{def:ring center}
Let $R$ be a ring.
The \emph{center} of $R$ is the subring of $R$
that contains all elements $c \in R$ such that
$c x = x c$ for every $x$ in $R$.
\end{definition}

I use the defintion style define the following environments: definition, problem, example, and assumption.
%%---------------------------------------------------%%
%| Define environments that use the definition style |%
%%---------------------------------------------------%%
\theoremstyle{definition}%
%%% Define definition environment %%%
\providetheorem{definition}{Definition}
\crefname{definition}{Definition}{Definitions}%
%%% Define problem environment %%%
\providetheorem{problem}{Problem}
\crefname{problem}{Problem}{Problems}%
%%% Define example environment %%%
\providetheorem{example}{Example}
% Add a mark at the end of each example.
\setEnvironmentQed{example}{\ensuremath{\blacksquare}}
%%% Define assumption environment %%%
% Note: We use singular "Assumption" even when there are
% multiple assumptions within a particular block.
\providetheorem{assumption}{Assumption}
\crefname{assumption}{Assumption}{Assumptions}
% Add a mark at the end of each assumption.
\setEnvironmentQed{assumption}{\ensuremath{\blacksquare}}
In definitions, you should emphasize the defined term to make it stand out.
The preferred way to do this is to surround the term with \emph{}, which will typically typeset the text in italics.
Unlike \textit{}, however, the \emph macro will switch to upright text if the surrounding text is already italicized, ensuring that the term highlighted even if you use italic text in your definition environments.
Remark Style
The remark style displays an italic label and upright body text.
\begin{remark}
Here is a remark.
\end{remark}

I use the remark style only for the remark environment.
%%-----------------------------------------------%%
%| Define environments that use the remark style |%
%%-----------------------------------------------%%
\theoremstyle{remark}%
%%% Define remark environment %%%
\providetheorem{remark}{Remark}
Chapter-based Numbering
For document classes that use chapters, I prefer to number the theorem-like environments on a chapter-by-chapter basis (e.g., “Theorem 1.1”, “Theorem 1.2” in Chapter 1 and “Theorem 2.1”, “Theorem 2.2” in Chapter 2.)
The following code automatically enables chapter-based numbering when the chapter counter is defined.
\ifcsname thechapter\endcsname
% If the document class uses chapters,
% then update numbering to use chapters.
\numberwithin{assumption}{chapter}
\numberwithin{definition}{chapter}
\numberwithin{remark}{chapter}
\numberwithin{example}{chapter}
\numberwithin{proposition}{chapter}
\numberwithin{theorem}{chapter}
\numberwithin{lemma}{chapter}
\numberwithin{corollary}{chapter}
\numberwithin{conjecture}{chapter}
\numberwithin{application}{chapter}
\fi
Unnumbered Environments
In some contexts, namely presentations, you may wish to use unnumbered environments (e.g., “Theorem” instead “Theorem 1”).
To omit theorem numbering, define theorem environments using \newtheorem* macro instead of \newtheorem.
If you already have theorem defined, you must use a different name for the unnumbered theorem environment, such as theorem*.
\newtheorem*{theorem*}{Theorem}
It is a bad idea, however, to have mixture of numbered and unnumbered theorems in the same document, so you may wish to simply replace \newtheorem{theorem}{Theorem} with \newtheorem*{theorem}{Theorem} so that \begin{theorem}...\end{theorem} inserts unnumbered theorems.
Proof Environment
The amsthm package also defines a proof environment.
I’ve found the default definition to be exactly how I want it, with a white square inserted at the end of the proof.
The usage is as follows:
\begin{proof}
It's true 'cause I say so.
\end{proof}

You can change the “proof” label by using an optional environment argument.
\begin{proof}[Proof Sketch]
This example is too small to contain the proof.
\end{proof}
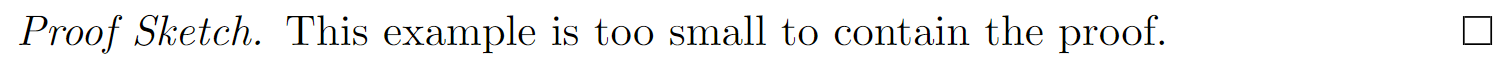
Using the optional argument is particularly useful if a theorem and its proof are separated by other text:
\begin{proof}[Proof of \cref{result:an earlier theorem}]
This proof does not occur immediately
after \cref{result:an earlier theorem}.
\end{proof}
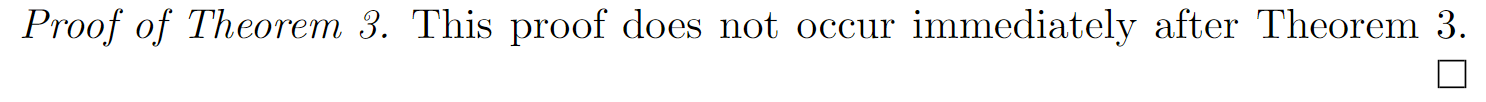 Note that the QED symbol in above example appears at the end of the next line because the first line fills the text width.
Note that the QED symbol in above example appears at the end of the next line because the first line fills the text width.
If the proof ends with an equation or a list, then the QED symbol will be placed below the equation or list, even if there is space to the side, which wastes space and looks bad:
\begin{proof}
The conclusion follow directly from this equation:
\[
1 + 1 = 2.
\]
\end{proof}
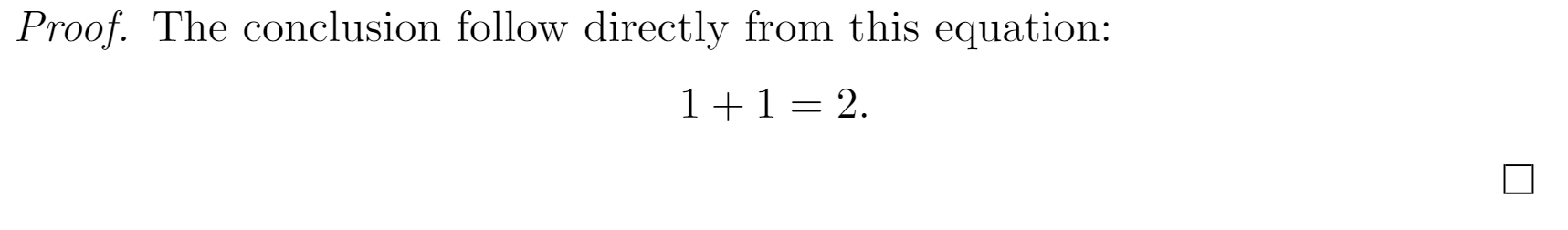
To fix this problem, place \qedhere inside the equation or list (at the end) to display the QED symbol at the correct location:
\begin{proof}
The conclusion follow directly from this equation:
\[
1 + 1 = 2. \qedhere
\]
\end{proof}